完全予約制
重心を理解する
重心とは、つり合いの取れる点。理学療法士の方なら、身体の重心が第二仙椎の前方にあることは常識でしょう。
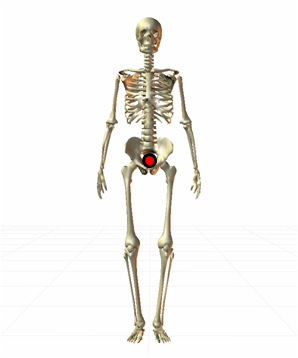
例えば、下図のとき、重心はどちらに移動しているでしょうか?
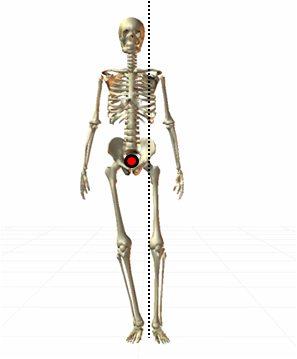
身体は左右対称ですから、重心が右側に移動していることは一目瞭然です。第二仙椎に重心があることを知らない人でも、簡単にわかります。
では、下図のとき、重心はどちらに移動しているでしょうか?
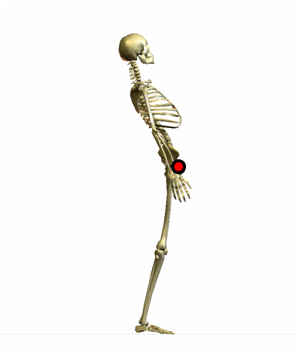
下半身は前方に移動していますが、上半身は後方に移動しています。第二仙椎の位置を診ても、重心の移動を判断できません。
このような姿勢分析では、せっかく学んだ知識が無意味です。重心を正しく理解して、臨床に役立てること。それが、本章の目的です。
重心を正しく理解すると言いましたが、当講座の対象は数学が苦手な方。力学の説明から始めたら、巷にある教科書と何も変わりません。そこで、重心を初めて習ったとき、つまり、中学校か高校で習った三角形の重心まで遡ってみることにしましょう。
| 問題1 三角形の重心を作図しなさい。  |
三角形の重心は、頂点とそれに向き合う辺の中点を結んだ線の交点です。
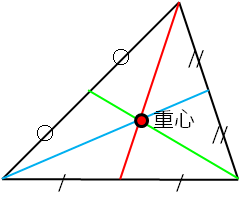
しかし、これでは、重心の意味を理解したことにはなりません。赤線で分かれる2つの三角形に注目して下さい。
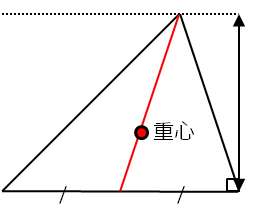
高さは共通で、底辺の長さは同じ。従って、2つの三角形の面積は、等しくなります。
三角形を回転させます。青線で分かれる2つの三角形は、どうなるでしょうか?
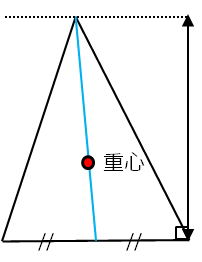
同じく、2つの三角形の面積は、等しくなります。
最後に、緑線で分かれた2つの三角形も、確認しておきましょう。
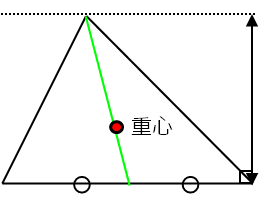
やはり、等しくなります。
従って、重心を通る直線は、その三角形を、面積の等しい三角形に分けることがわかりました。
この問題のポイントは、つり合いの意味です。
重心は、何と何のつり合いを取っているのでしょうか?また、つり合いの基準は何でしょうか?それがわかっていなければ、重心を理解することはできません。
ここで、力学の視点を加えます。三角形が、薄い均一の板としましょう。重心を通る直線は、面積を等しく分けるため、重さも等しく分けます。従って、重心は2つの三角形と三角形のつり合いを取っている。そして、その基準は、三角形の重さであると考えることができます。
ただし、重さが基準であることは、まだ事実とは言えません。なぜなら、重心を通る直線は、他にもたくさん引けるからです。重心を通る全ての直線が三角形の重さを半分にすると証明されたとき、初めて事実と言えます。
その証明は、問題3までお待ち下さい。
| 問題2 四角形の重心を作図しなさい。 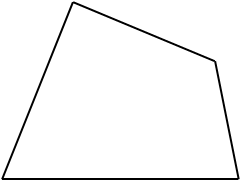 |
四角形は、必ず2つの三角形に分かれます。
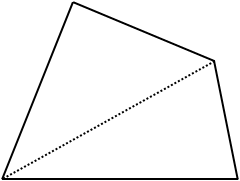
分けた三角形の重心を求めて、重心同士を結んでみましょう。
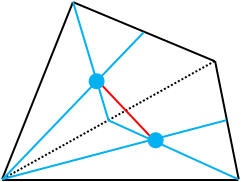
これは、四角形の重心が、2つの三角形の重心を結ぶ直線上にあることを表しています。
今度は、別の2つの三角形に分けます。同じように、重心を求めて、重心同士を結んで下さい。
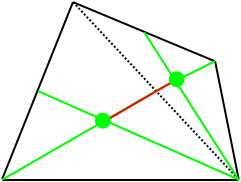
同様に、四角形の重心が、2つの三角系の重心を結ぶ直線上にあることを表しています。
従って、2つの直線の交点が、四角形の重心となります。
どんな多角形も、必ず三角形に分かれます。従って、上記の方法を繰り返せば、どんな多角形の重心も作図することができます。
ここで、力学の重心の定義を紹介します。
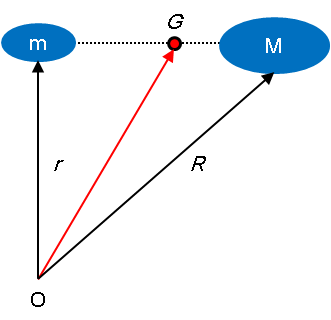
上図のとき、重心ベクトルGは、次式で定義されます。
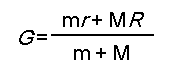
力学ではベクトルを使って重心を表しますが、意味は作図と同じです。だから、難しい数学を知らなくても、物理を理解することはできるのです。
| 問題3 AB=AC、BC=9、高さ12の二等辺三角形がある。ただし、DEは、重心Gを 通り、BCに平行な直線とする。  1)重心Gを作図しなさい。 2)AGとGF、DEの長さを定規で測りなさい。 3)三角形AEDと台形BCDEの面積を求めなさい。 |
1)は、問題1と同じです。
2)は、AG=8、GF=4、DE=6となります。
三角形の重心は頂点と中点を結ぶ直線を2:1に内分することを知っていれば、定規で測らなくても、AGとGFを計算できます。
また、三角形ABC∽三角形AEDに気付けば、DEも計算できます。
3)は、三角形AED=24、台形BCDE=30となります。
台形の面積の求め方は、(上底+下底)×高さ÷2ですから
台形BCDE=(6+9)×4÷2
=30
と計算できます。
この結果から、重心を通る直線の中に、三角形の重さを半分にしない直線があることが証明されました。従って、つり合う基準は、重さでありません。
改めて、つり合う基準を考えます。三角形AEDの重心Pと、台形BCDEの重心Qを求めてみましょう。対称性から、PとQは、AF上にあることは明らかです。
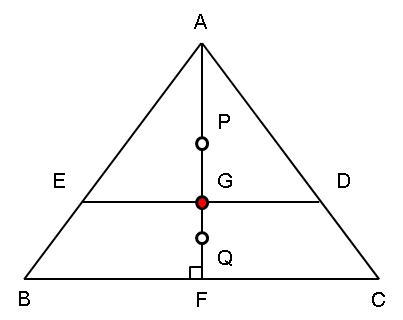
三角形の重心の性質から、AGを2:1に内分する点がPになります。
台形の重心は、高さを(上底+下底×2):(上底×2+下底)に内分する点になります。従って、GFを8:7に内分する点がQになります。
上図を回転させます。
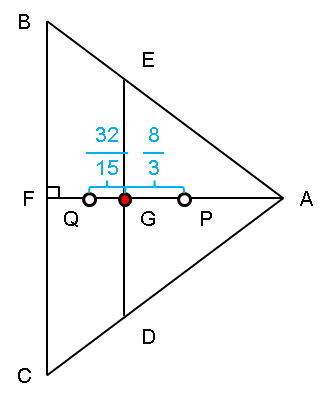
台形BCDEの面積は30、三角形AEDの面積は24ですから
台形BCDEの面積×QG=三角形AEDの面積×GP
が成立します。
これは、テコのつり合いと同じです。
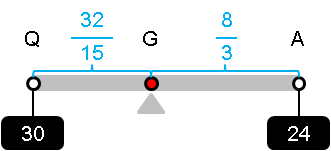
従って、つり合いの基準は、重さ×重心間の距離と結論付けられます。問題1で分かれた2つの三角形は、偶然、重心間の距離まで等しかったのです。
この問題のポイントは、2つあります。
まず、つり合いの基準が、テコと同じであること。力学では、モーメントという物理量がつり合っていると考えます。モーメントの詳細は、別章で説明します。
次に、重心は、形や大きさを無視できること。テコと見なす前、そこには台形と三角形が存在していました。しかし、テコと見なした瞬間から、図形の形に関係なく、重さと重心間の距離だけで、つり合いが決まります。
今度は、身体をテコと見なしてみましょう。
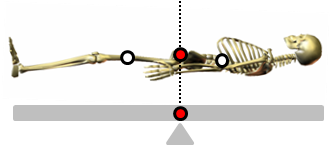
上図では、上半身と下半身がつり合っています。このとき、
上半身の重さ×重心間の距離=下半身の重さ×重心間の距離
が成立します。
ただし、図形とは異なり、姿勢は変化します。重心間の距離も変わるため、つり合う条件も同じとは限りません。このため、合成重心の求め方を理解する必要があるのです。
合成重心とは、各分節の重心から導かれた全体の重心のこと。次の問題で、その合成重心の求め方を練習してみましょう。
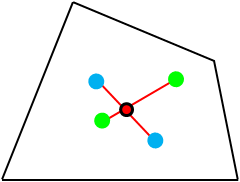
| 問題4 分節の質量比を、大腿:下腿:足部=10:5:1とする。下図に示す分節の 重心を参考にして、下肢の合成重心を作図しなさい。 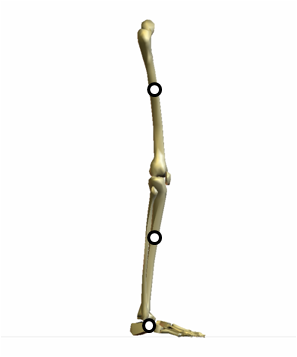 |
重さ×重心間の距離が等しくなるとき、つり合います。言い換えれば、重心間の距離は、重さの逆数に比例するわけです。
大腿と下腿の重心を直線で結びます。
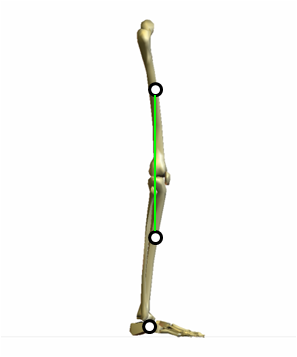
質量比は大腿:下腿=10:5ですから、重心間の距離を5:10に内分する点が大腿と下腿の合成重心になります。
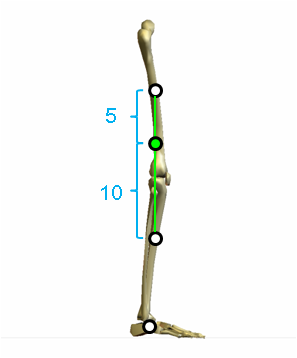
同様に、合成重心と足部の重心を直線で結びます。
質量比は10+5:1=15:1ですから、重心間の距離を1:15に内分する点が下肢の合成重心になります。
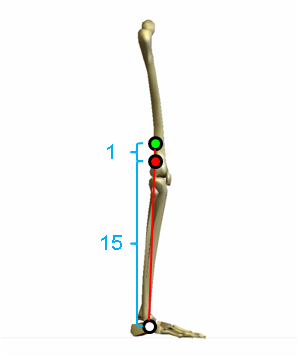
分節の重心の位置は、姿勢に影響されません。重心の位置は、分節の近位端から大腿と下腿は40%、足部は50%にあります。従って、各分節の重さと重心の位置を知っていれば、下図のような肢位の場合でも、全く同じ方法で合成重心を求めることができます。
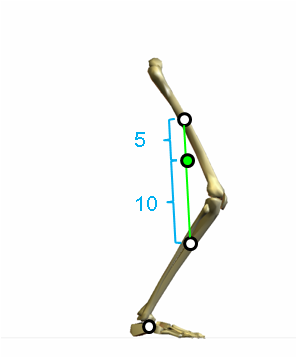
ただし、面倒だからと言って、下図の三角形の重心を求めてはいけません。
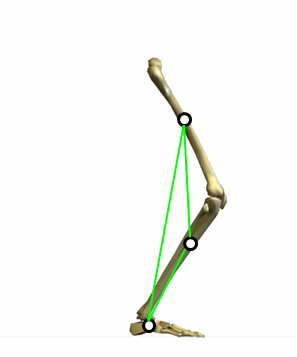
三角形の重心は、頂点にかかる重さが全て等しくなるときだけ、合成重心に一致します。上図の場合、大腿と下腿、足部の重さはバラバラですから、合成重心に一致しないのです。
さらに勉強されたい方は、松井秀治氏の「運動と身体の重心」を読まれることをお勧めします。
| 問題5 質量比を、上半身:下半身=3:2とする。下図に示す分節の重心を参考に して、重心の移動方向を答えなさい。  |
問題4と同様に、上半身と下半身の重心を直線で結びます。
質量比は3:2ですから、重心間の距離を2:3に内分する点が重心です。
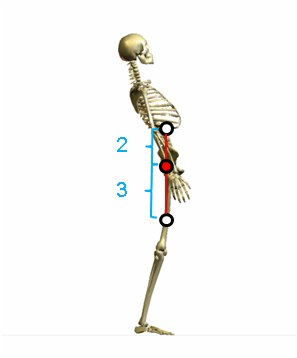
姿勢変化の前後を比べてみましょう。
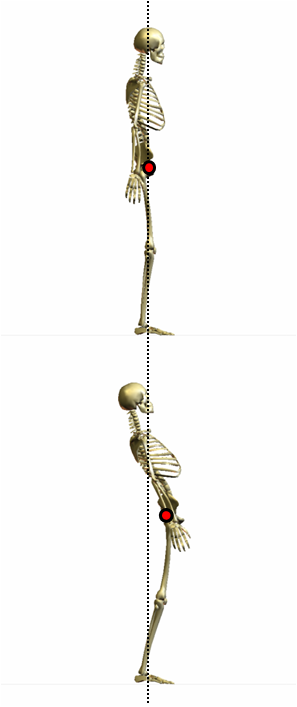
従って、重心は前方に移動したことがわかりました。
分節の数が増えるほど、合成重心の精度は高くなります。より詳細な姿勢分析を求める方は、分節の数を増やしてみるとよいでしょう。



